本文章将介绍CTF-Crypto类的几种题型,包括古典密码单多表加密,RSA和ECC等。希望能帮助刚入门的CTFer了解密码学的一些套路。
古典密码(Classical Cipher)
古典密码分为两种:代替密码(Substitution Cipher)和换位密码(Transposition Ciphers)。像常见的凯撒密码(Caesar Cipher)、ROT5、ROT13、ROT18和仿射密码(Affine Cipher)都是单表代替密码(Mono-alphabetic Cipher),而像栅栏密码(Rail-fence Cipher)则为换位密码。
单表代替密码无法防御字母和单词频率分析,例如英语中出现最多的字母为E、T、A,那么经过单表加密后其相对应地字母频率也会保持一致。例如:
原文:
the first well-documented description of a polyalphabetic cipher was formulated by leon battista alberti around 1467 and used a metal cipher disc to switch between cipher alphabets.
仿射密码加密后:
omf qxsdo vfee-uljzpfaofu ufdjsxwoxla lq n wlernewmnyfoxj jxwmfs vnd qlspzenofu yr efla ynooxdon neyfsox nslzau 1467 nau zdfu n pfone jxwmfs uxdj ol dvxojm yfovffa jxwmfs newmnyfod.
原文中出现过18次e,而密文中f的次数也为18次。
由于CTF中大多数题目只会用到英文的26个字母,所以此类加密方法可以暴力破解。网上有很多此类的网站。例如:(http://www.quipqiup.com/)。
多表代替密码
比较具有代表性的多表代替密码是维吉尼亚密码(Vigenere Cipher)。这种密码是根据密钥对明文中的每一个字符进行不同的偏移,在字母表下,明文和密钥的加密公式为:
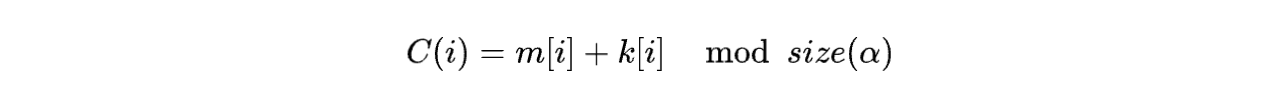
为了方便英文加密,一般会使用以下加密表:

图1:维吉尼亚密码概述图(来源:https://baike.baidu.com/item/维吉尼亚密码/4905472?fr=aladdin)
假设明文为:
VIGENERECIPHER
密钥为:
ABCDEFGHIJKLMN
则密文为:
VJIHRJXLKRZSQE
如果密钥长度大于等于明文且为一次性,则理论上无法破译。在CTF中,一般会出现两种情况:
密文极短,有明显的字符提示
例如:密文ivdq{W1_PLQKDLXJ}中的ivdq大概率是对应flag,可以通过计算推算出密钥。这种情况逆推很简单,甚至暴力破解都可以。
密文很长,密钥会重复。
在密文很长的情况下,寻找关键字就成了找到密钥突破口的关键,同时可以寻找密文中重复字段以计算出密钥长度(这种方法被称为卡西斯基实验(Kasiski examination))。
攻防世界crypto区的shanghai就是这样的一道题目。题目给出了以下密文并明示是维吉尼亚密码:
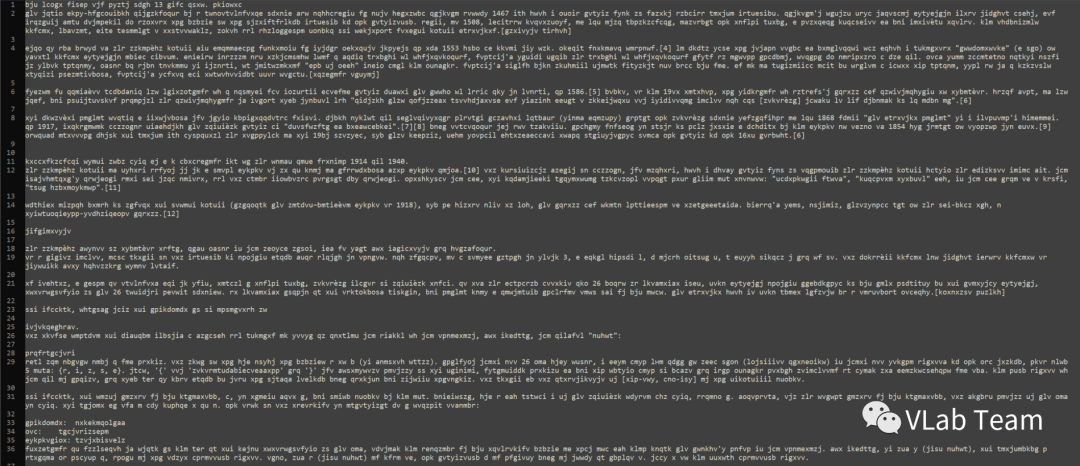
首先发现文章中有很多4位数字且既有可能是年份。搜索1的时候可以发现以下这段:
kxccxfkzcfcqi wymui zwbz cyiq ej e k cbxcregmfr ikt wg zlr wnmau qmue frxnimp 1914 qil 1940.
这里大概率是between 1914 and 1940,那么反推密钥可以发现 frxnimp - between = enereic, qil - and = qvi。 那么密钥至少是enereicqvi。其次,文中多次出现[1]这样的引用,可以推断出这极有可能是从维基百科上扒下来的文章。那么密文中出现的[gzxivyjv tirhvh]和[xqzegmfr vguymj]大概率是[citation needed],所以:
gzxivyjv tirhvh - citation needed = ereicqvi genere
xqzegmfr vguymj - citation needed = vigenere icqvig
由此可见,密钥的内容为ereicqvigen。剩下的只需要确认顺序即可(最终密钥为icqvigenere)。
以上方法是笔者在做这道题的时候的思路,但是这种思路可能较为跳脱,在CTF现场很难想到,那么有没有简单粗暴的方法来解决这类题目呢?
上面讨论的古典密码的本质是对文字进行某种程度的偏移,这就表示这种加密无法隐藏语言本身的统计特性,只要知道明文的语言且密文够长的话,这种加密在概率论面前不堪一击。
这里暂且默认明文语言是英文以方便讨论。
上面讲单表替换密码的时候提到过可以通过分析字母频率破解单表替换密码,这是因为在正常语义的文本中每个字母的出现次数会有显著差异。维基百科上给出了每个字母在英文中出现的频率(来源:维基百科https://zh.wikipedia.org/wiki/%E5%AD%97%E6%AF%8D%E9%A2%91%E7%8E%87):
| 字母 | 英语中出现的频率 |
|---|---|
| a | 8.167% |
| b | 1.492% |
| c | 2.782% |
| d | 4.253% |
| e | 12.702% |
| f | 2.228% |
| g | 2.015% |
| h | 6.094% |
| i | 6.966% |
| j | 0.153% |
| k | 0.772% |
| l | 4.025% |
| m | 2.406% |
| n | 6.749% |
| o | 7.507% |
| p | 1.929% |
| q | 0.095% |
| r | 5.987% |
| s | 6.327% |
| t | 9.056% |
| u | 2.758% |
| v | 0.978% |
| w | 2.360% |
| x | 0.150% |
| y | 1.974% |
| z | 0.074% |
可以看到字母e,t,a的出现频率远远大于其他字母,这种性质也会在密文中保留,为了将这种性质量化,在这里先引入一个概念:一段文字的重合指数(Index of Coincidence):
设为每个字母在此段文字中出现的次数,为字母总数,则该文字的重合指数的定义为:
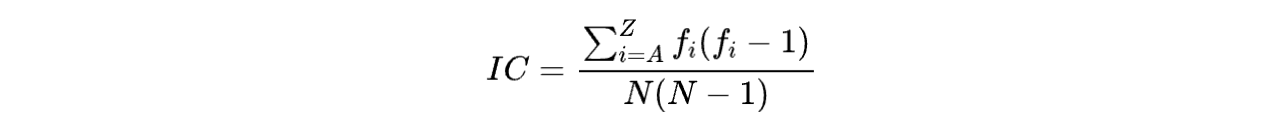
如果这个定义看起来比较抽象,可将其理解为在一段文字中两个字母相似的可能性。根据英文统计的数据,一段正常语义的英文文本的IC值应该在0.065左右,而一段随机生成的文本IC值应在0.038。同时注意,当一段文字通过单表加密(平移)后,其IC值不变。
通过以上定义就可以寻找密钥长度。可配合以下例子理解思路:
明文:
ABCDEF
密钥:
ABC
密文:
ACEDFH
如果将密文分为AD,CF,EH,则他们和原文的对应字母(AD,BE,CF)形成单表加密(AD->AD,BE->CF,CF->EH)。通过这种分类,可以将多表加密转成了多个单表加密。由于单表加密不会改变IC值,且一般英文文本的IC值为0.065,如果将一段密文以这种方法分成d组且每组的IC值都接近0.065,基本可以确定d就是密钥长度。
还是以shanghai的密文为例,去掉所有空格和非字母字符后可以发现:
| d | IC值 |
|---|---|
| 7 | 0.044291254817570604 0.041150462203093784 0.042921463974095554 0.04293418844060784 0.04321055390955534 0.044974415873131994 0.04360071692454003 |
| 8 | 0.043860067265167765 0.04438971425544874 0.04455920129233865 0.041942745160350625 0.041905669871030955 0.041505704311045694 0.04355681196231488 0.04398191199366601 |
| 9 | 0.04150511280310183 0.04477302100702466 0.044652483409338986 0.04324360654635884 0.04273280236582989 0.045522062035823506 0.04589844406358168 0.04187922169573546 0.04202708606378331 |
| 10 | 0.0453860546752107 0.045005215836272414 0.042355902174093026 0.041494875233884725 0.042099249913069396 0.041875714072823006 0.04545228751676519 0.04330188287127478 0.042412402843010934 0.04359283428238913 |
| 11 | 0.06754547004945777 0.0728122711449524 0.06835806221847694 0.06485689349023385 0.06796681413709733 0.06472647746310731 0.06764579007032434 0.06763575806823768 0.06118518072651759 0.07476851155185041 0.0650976615403136 |
| 12 | 0.042709762060945795 0.04211342357922357 0.042864810066193575 0.04336573439084024 0.04301985807144135 0.042685908521676905 0.046252012642375814 0.04111157492993023 0.042864810066193575 0.04179251162567717 0.04511242149671604 0.04506448055995014 |

这里pα为表1中字母α对应的百分比。
同样以shanghai的密文为例,算出密钥长度为11后可通过以上步骤可以得出密钥为icqvigenere。
此外,参赛者还可以使用 https://www.guballa.de/vigenere-solver 来解密。
小结
古典密码的题目多为脑洞题,一般出题者会在题目中给出一点提示(例如上面的题目)。只要知识储备充足,这类题目就不算难题。网上有很多关于古典密码的总结(例如:http://www.cnblogs.com/daban/p/5680451.html)供参赛者阅览。
只要断定是古典密码题,笔者建议先尝试先找一下密文规律,尝试一下单多表(凯撒和维吉尼亚)替换,然后再去套其他加密方式。加解密可以使用(http://www.atoolbox.net/Category.php?Id=27),感谢此工具箱的开发者。
编码(Encoding)
严格意义上来说,编码并不算一种加密方式,所以笔者认为将纯编码题归于Crypto是很错误的行为(最多归于Misc)。本章节中只会讨论一些常见编码(base16/32/64等)的识别方式。
Base家族
一种比较常见的编码方式是base家族,像base64,base32不管是CTF还是工作中都会用到。如果发现某段文字的结尾有“=”,则该段文字既有可能是base32(如果只有大写)/64(如果有“+”、“/”)编码。其他base家族包含base58,base91等。这里推荐mufeedvh的basecrack(https://github.com/mufeedvh/basecrack),直接把输入丢进去就可以知道原文和加密用的base了。
Unicode/HTML编码
此类编码的特征为“&#DDD;&#DDD”(十进制)或“&#xHH;&#xHH”(十六进制)。Unicode还有一种”\U”和 “\U+”的格式
Escape/Unescape/URL/Hex编码
此类编码都以“%”开头,如果是“%u”那就是Escape/Unescape编码,不然就是URL或Hex编码
在CTF中编码一般与古典密码同时出现,一般是先用古典密码加密一遍,然后再利用某种编码转换一次(或者多次,看出题者心情)。在现代密码题目中出现的编码基本都是base家族编码,python有内置库进行转换,所以这里就不在赘述。
小结
现在CTF中纯编码题目越来越少,如果有的话一般是用来凑数和送分的。这类题目考验的是参赛者的百度(谷歌)能力,像与佛论禅、社会主义编码这种一百度(谷歌)就能搜到加解密工具。如果真的遇到纯编码题,请参考(https://www.cnblogs.com/ruoli-s/p/14206145.html,https://blog.csdn.net/dyw_666666/article/details/89973048)等文章,根据特征一步步转换即可。这里也希望出题人可以少出一些编码题,做的真的没意思。
现代密码(Modern Cryptography)
现代密码和古典密码的侧重点不同,现代密码利用较为复杂的加密机制。某些非对称加密法是利用目前数学上暂未解决的课题保证安全性,像RSA便是依赖大整数(大于4096比特)的质因数分解较为困难,ECC依赖于椭圆曲线离散对数计算困难等问题保证安全性。如果有一天上述问题有了快速解,那么现代密码学将会有一次大洗牌。而现代对称加密法,例如AES,DES,RC4等(至少在发表时)则是从概率学上证明了他们的安全性,但有些算法因为算力的飞速增长和一些非常规破解方法被淘汰。DES、3DES就是因为算力的飞速增长而被淘汰的算法(取代他们的是AES)。
现代密码学是CTF的重点,也是笔者认为最有意思的地方。此类题目更多考验的是参赛者的数学能力而不是对加密算法的掌握能力,同时,此类题目还可以和reverse,pwn类题合并,考验参赛者的综合能力。
RSA

了解了RSA的加密过程,可以发现,这种RSA的安全隐患主要是集中于质数的生成方式和大小,同时,由于c和m是一对一的关系(同样的c会导致同样的m),这使得这个版本的RSA(在使用同样的公密钥情况下)无法防御唯密文攻击,已知明文攻击,选择明文攻击和选择密文攻击。
有了以上知识,下面对于RSA的简单攻击就很容易理解了。
RSA的一些简单攻击

给了多个N

下面是一个例子:
import gmpy2
n1=9051013965404084482870087864821455535159008696042953021965631089095795348830954383127323853272528967729311045179605407693592665683311660581204886571146327720288455874927281128121117323579691204792399913106627543274457036172455814805715668293705603675386878220947722186914112990452722174363713630297685159669328951520891938403452797650685849523658191947411429068829734053745180460758604283051344339641429819373112365211739216160420494167071996438506850526168389386850499796102003625404245645796271690310748804327
n2=13225948396179603816062046418717214792668512413625091569997524364243995991961018894150059207824093837420451375240550310050209398964506318518991620142575926623780411532257230701985821629425722030608722035570690474171259238153947095310303522831971664666067542649034461621725656234869005501293423975184701929729170077280251436216167293058560030089006140224375425679571181787206982712477261432579537981278055755344573767076951793312062480275004564657590263719816033564139497109942073701755011873153205366238585665743
p = gmpy2.gcd(n1,n2)
print("p: "+str(p))
q1 = n1/p
q2 = n2/p
print("q1: "+str(q1))
print("q2: "+str(q2))
结果:
p: 1564859779720039565508870182569324208117555667917997801104862601098933699462849007879184203051278194180664616470669559575370868384820368930104560074538872199213236203822337186927275879139590248731148622362880471439310489228147093224418374555428793546002109
q1: 5783913729972248046257748237381036166340510237175309134215544535161825064662282453337784448005284808837580018485416822432532984866837614690163367627041287361695241110587309279278895270988005344997579717771026011337608229756076523535761543537434050411622003
q2: 8451842502173444137736814762941916058188287492225312470701776645749560167356046185751987142378046260660654109657367986531032438683223878564614629060680414105738103196373377352503582154146395466843322435064918174001568589071204760456484430101336520922543227
RSA的一些进阶攻击
广播攻击

import gmpy2
from Crypto.Util.number import long_to_bytes, bytes_to_long
def crt(s):
N = 1
for c,n in s:
N *= n
res = 0
for c,n in s:
g,s,t = gmpy2.gcdext(n,N/n)
if g != 1:
N=N/n
continue
res += c*t*N/n
return res % N
data=[{"c": 7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n": 25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},
{"c": 21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n": 23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},
{"c": 6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n": 18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},
{"c": 4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n": 23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},
{"c": 22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n": 31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},
{"c": 17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n": 22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},
{"c": 1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n": 25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},
{"c": 15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n": 32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},
{"c": 8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n": 52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},
{"c": 13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n": 30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]
l = [(d['c'],d['n']) for d in data]
x = crt(l)
print(long_to_bytes(gmpy2.iroot(x,10)[0]))
孙子定理在很多RSA题目中都会出现,建议不了解的参赛者仔细研究一下。
Wiener’s Attack
此攻击由Michael J. Wiener提出,其定理为:
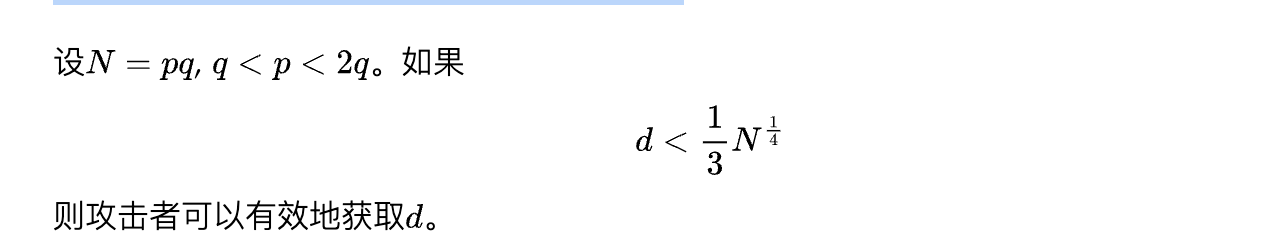
此定理的证明涉及连分数和连分数的收敛。有兴趣的可以参考维基百科中的证明(https://en.wikipedia.org/wiki/Wiener's_attack)
如果题目中e的值非常大,那么此攻击大概率会奏效。具体实现细节可参照https://github.com/pablocelayes/rsa-wiener-attack 或者直接修改RSAwienerHacker.py即可。
Coppersmith攻击

from sage.all import *
import binascii
n = 0x.... # 此处为16进制数
p4 =0x.... #p的高位 16进制
cipher = 0x 密文
e2 = 0xf93b
pbits = 1024
kbits = pbits - p4.nbits()
print p4.nbits()
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
p = p4+int(roots[0])
print "p: ", hex(int(p))
assert n % p == 0
q = n/int(p)
print "q: ", hex(int(q))
print gcd(p,q)
phin = (p-1)*(q-1)
print gcd(e2,phin)
d = inverse_mod(e2,phin)
flag = pow(cipher,d,n)
flag = hex(int(flag))[2:-1]
print binascii.unhexlify(flag)
(来源:https://github.com/wy666444/Crypto/blob/master/RSAHitBit/Untitled/sage爆破后八位.sage)
这里用Factoring with High Bits Known的来做一道题(某城杯的CTF):
from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 724
hint2 = q % (2 ** 265)
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)

import gmpy2
p0 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
q0 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
p1=n*gmpy2.invert(q0,2**265) % (2**265)
PR.<x> = PolynomialRing(Zmod(n))
f = ((p0 << 724) + p1) + x*(2**265)
f = f.monic()
r = f.small_roots(X=2^(1024-300-265),beta=0.4)
print(r)
结果:
[]
看来需要知道更多比特,那就进行爆破吧:
from gmpy2 import *
p0 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
q0 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
p1=n*gmpy2.invert(q0,2**265) % (2**265)
PR.<x> = PolynomialRing(Zmod(n))
found = False
for i in range(10):
for j in range(2**i):
f = (((p0<<724) + p1) + j* (2**265)) + x*(2**265)*(2**i)
f = f.monic()
r = f.small_roots(X=2^(1024-300-265-i),beta=0.4)
if(pp):
print(i)
print(j)
print(r)
print(((p0<<724) + p1) +j*(2**265)+r[0]*(2**265)*(2**i))
found = True
break
if(found):
break
结果:
5
19
[15828499362967398696211792235007306181119418193082672642200577556639039538935915318382610283676414741804355911153213893405885406343674296]
133637329398256221348922087205912367118213472434713498908220867690672019569057789598459580146410501473689139466275052698529257254973211963162087316149628000798221014338373126500646873612341158676084318494058522014519669302359038980726479317742766438142835169562422371156257894374341629012755597863752154328407
看来在爆破的话需要至少570位比特。
小结
现在CTF里面RSA的题目已经很少见到简单攻击了,网上也有很多关于简单攻击的文章(例如:https://blog.csdn.net/huanghelouzi/article/details/82943615)。感兴趣的可以自行搜索。Dan Boneh对所有的攻击进行了比较系统的整理供参考(https://www.ams.org/notices/199902/boneh.pdf)
ECC


print 'Try to solve the 3 ECC'
from secret import flag
from Crypto.Util.number import *
assert(flag[:5]=='flag{')
flag = flag[5:-1]
num1 = bytes_to_long(flag[:7])
num2 = bytes_to_long(flag[7:14])
num3 = bytes_to_long(flag[14:])
def ECC1(num):
p = 146808027458411567
A = 46056180
B = 2316783294673
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
def ECC2(num):
p = 1256438680873352167711863680253958927079458741172412327087203
#import random
#A = random.randrange(389718923781273978681723687163812)
#B = random.randrange(816378675675716537126387613131232121431231)
A = 377999945830334462584412960368612
B = 604811648267717218711247799143415167229480
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
'''
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
print primes
dlogs = []
for fac in primes:
t = int(int(P.order()) / int(fac))
dlog = discrete_log(t*Q,t*P,operation="+")
dlogs += [dlog]
print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
print num
print crt(dlogs,primes)
'''
def ECC3(num):
p = 0xd3ceec4c84af8fa5f3e9af91e00cabacaaaecec3da619400e29a25abececfdc9bd678e2708a58acb1bd15370acc39c596807dab6229dca11fd3a217510258d1b
A = 0x95fc77eb3119991a0022168c83eee7178e6c3eeaf75e0fdf1853b8ef4cb97a9058c271ee193b8b27938a07052f918c35eccb027b0b168b4e2566b247b91dc07
B = 0x926b0e42376d112ca971569a8d3b3eda12172dfb4929aea13da7f10fb81f3b96bf1e28b4a396a1fcf38d80b463582e45d06a548e0dc0d567fc668bd119c346b2
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
ECC1(num1)
print '=============='
ECC2(num2)
print '=============='
ECC3(num3)
三个ECC加密对应了三个破解方法。一个个来看一下:
def ECC1(num):
p = 146808027458411567
A = 46056180
B = 2316783294673
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
这里的数比较小,可以直接用sagemath的discrete_log来解
p = 146808027458411567
A = 46056180
B = 2316783294673
E = EllipticCurve(GF(p), [A, B])
P = E(119851377153561800, 50725039619018388, 1)
Q = E(22306318711744209, 111808951703508717, 1)
print(discrete_log(Q, P, operation='+'))
结果:
13566003730592612
接着看第二个ECC:
def ECC2(num):
p = 1256438680873352167711863680253958927079458741172412327087203
#import random
#A = random.randrange(389718923781273978681723687163812)
#B = random.randrange(816378675675716537126387613131232121431231)
A = 377999945830334462584412960368612
B = 604811648267717218711247799143415167229480
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
'''
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
print primes
dlogs = []
for fac in primes:
t = int(int(P.order()) / int(fac))
dlog = discrete_log(t*Q,t*P,operation="+")
dlogs += [dlog]
print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
print num
print crt(dlogs,primes)
'''


p = 1256438680873352167711863680253958927079458741172412327087203
A = 377999945830334462584412960368612
B = 604811648267717218711247799143415167229480
E = EllipticCurve(GF(p),[A,B])
P = E(550637390822762334900354060650869238926454800955557622817950, 700751312208881169841494663466728684704743091638451132521079)
Q = E(1152079922659509908913443110457333432642379532625238229329830, 819973744403969324837069647827669815566569448190043645544592)
n = E.order()
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
print(primes) #[2, 27, 5, 7, 212117, 302426983]
ks = []
for p in primes:
P0 = (n // p) * P
Q0 = (n // p) * Q
ks.append(P0.discrete_log(Q0))
k = crt(ks, primes)
print(k)
这里稍微简化了一下步骤,只做了一次。不影响结果:
[2, 27, 5, 7, 212117, 302426983]
16093767336603949
最后一个ECC
def ECC3(num):
p = 0xd3ceec4c84af8fa5f3e9af91e00cabacaaaecec3da619400e29a25abececfdc9bd678e2708a58acb1bd15370acc39c596807dab6229dca11fd3a217510258d1b
A = 0x95fc77eb3119991a0022168c83eee7178e6c3eeaf75e0fdf1853b8ef4cb97a9058c271ee193b8b27938a07052f918c35eccb027b0b168b4e2566b247b91dc07
B = 0x926b0e42376d112ca971569a8d3b3eda12172dfb4929aea13da7f10fb81f3b96bf1e28b4a396a1fcf38d80b463582e45d06a548e0dc0d567fc668bd119c346b2
E = EllipticCurve(GF(p),[A,B])
P = E.random_point()
Q = num*P
print E
print 'P:',P
print 'Q:',Q
乍一看数字都很大,前两种方法一定不行。但是通过计算发现:
p = 0xd3ceec4c84af8fa5f3e9af91e00cabacaaaecec3da619400e29a25abececfdc9bd678e2708a58acb1bd15370acc39c596807dab6229dca11fd3a217510258d1b
A = 0x95fc77eb3119991a0022168c83eee7178e6c3eeaf75e0fdf1853b8ef4cb97a9058c271ee193b8b27938a07052f918c35eccb027b0b168b4e2566b247b91dc07
B = 0x926b0e42376d112ca971569a8d3b3eda12172dfb4929aea13da7f10fb81f3b96bf1e28b4a396a1fcf38d80b463582e45d06a548e0dc0d567fc668bd119c346b2
E = EllipticCurve(GF(p),[A,B])
P = E(10121571443191913072732572831490534620810835306892634555532657696255506898960536955568544782337611042739846570602400973952350443413585203452769205144937861,8425218582467077730409837945083571362745388328043930511865174847436798990397124804357982565055918658197831123970115905304092351218676660067914209199149610)
Q = E(964864009142237137341389653756165935542611153576641370639729304570649749004810980672415306977194223081235401355646820597987366171212332294914445469010927,5162185780511783278449342529269970453734248460302908455520831950343371147566682530583160574217543701164101226640565768860451999819324219344705421407572537)
n = E.order()
print(n) #11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419
print(p) #11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419

def HenselLift(P,p,prec):
E = P.curve()
Eq = E.change_ring(QQ)
Ep = Eq.change_ring(Qp(p,prec))
x_P,y_P = P.xy()
x_lift = ZZ(x_P)
y_lift = ZZ(y_P)
x, y, a1, a2, a3, a4, a6 = var('x,y,a1,a2,a3,a4,a6')
f(a1,a2,a3,a4,a6,x,y) = y^2 + a1*x*y + a3*y - x^3 - a2*x^2 - a4*x - a6
g(y) = f(ZZ(Eq.a1()),ZZ(Eq.a2()),ZZ(Eq.a3()),ZZ(Eq.a4()),ZZ(Eq.a6()),ZZ(x_P),y)
gDiff = g.diff()
for i in range(1,prec):
uInv = ZZ(gDiff(y=y_lift))
u = uInv.inverse_mod(p^i)
y_lift = y_lift - u*g(y_lift)
y_lift = ZZ(Mod(y_lift,p^(i+1)))
y_lift = y_lift+O(p^prec)
return Ep([x_lift,y_lift])
def SmartAttack(P,Q,p,prec):
E = P.curve()
Eqq = E.change_ring(QQ)
Eqp = Eqq.change_ring(Qp(p,prec))
P_Qp = HenselLift(P,p,prec)
Q_Qp = HenselLift(Q,p,prec)
p_times_P = p*P_Qp
p_times_Q=p*Q_Qp
x_P,y_P = p_times_P.xy()
x_Q,y_Q = p_times_Q.xy()
phi_P = -(x_P/y_P)
phi_Q = -(x_Q/y_Q)
k = phi_Q/phi_P
k = Mod(k,p)
return k
p = 0xd3ceec4c84af8fa5f3e9af91e00cabacaaaecec3da619400e29a25abececfdc9bd678e2708a58acb1bd15370acc39c596807dab6229dca11fd3a217510258d1b
A = 0x95fc77eb3119991a0022168c83eee7178e6c3eeaf75e0fdf1853b8ef4cb97a9058c271ee193b8b27938a07052f918c35eccb027b0b168b4e2566b247b91dc07
B = 0x926b0e42376d112ca971569a8d3b3eda12172dfb4929aea13da7f10fb81f3b96bf1e28b4a396a1fcf38d80b463582e45d06a548e0dc0d567fc668bd119c346b2
E = EllipticCurve(GF(p),[A,B])
P = E(10121571443191913072732572831490534620810835306892634555532657696255506898960536955568544782337611042739846570602400973952350443413585203452769205144937861,8425218582467077730409837945083571362745388328043930511865174847436798990397124804357982565055918658197831123970115905304092351218676660067914209199149610)
Q = E(964864009142237137341389653756165935542611153576641370639729304570649749004810980672415306977194223081235401355646820597987366171212332294914445469010927,5162185780511783278449342529269970453734248460302908455520831950343371147566682530583160574217543701164101226640565768860451999819324219344705421407572537)
n = E.order()
k = SmartAttack(P,Q,p,8)
print(k)
结果:
19597596255129283097357413993866074145935170485891892
将三个解出来的数合并在一起就是flag了。
小结
ECC加密相比RSA更复杂一些,需要参赛者有很好的数学基础去了解攻击手法,至少需要了解攻击手法的使用条件才可以很好的面对这类题目。
结语
笔者第一次接触CTF是在大三刚开始接触安全的时候,当时被这种Jeopardy-like形式的比赛吸引了,但由于学业繁重加上自身懒散并未深入了解。加入墨云科技后参加了几次CTF,凭着在学校学过的一些密码学知识和平时刷题也做出了一些密码学题目。在笔者参加的几次CTF中,笔者发现密码学题目质量参差不齐,甚至某CTF的密码学题目竟然全是网络上可以搜到的原题。为了让参赛者早日摆脱简单RSA,古典密码等初级题目并将精力放在其他难题上,在此文章中,笔者简单地梳理密码学的一些套路。希望此文章可以帮助刚入门的CTFer了解密码学,也希望出题人能够避开本文章中的套路并出一些新颖的题目。
由于笔者才疏学浅,难免会有遗漏和错误。欢迎诸位大佬指出。
参考文献
Boneh D. Twenty years of attacks on the RSA cryptosystem[J]. Notices of the AMS, 1999, 46(2): 203-213. Galbraith, Steven D. Mathematics of public key cryptography. Cambridge University Press, 2012. Novotney P. Weak Curves In Elliptic Curve Cryptography[J]. modular. math. washington. edu/edu/2010/414/projects/novotney. pdf, 2010.
参考网站
https://hgarrereyn.gitbooks.io/th3g3ntl3man-ctf-writeups/content/2017/picoCTF_2017/problems/cryptography/ECC2/ECC2.html https://weichujian.github.io/2020/05/27/Ecc椭圆曲线基础/ https://ctf-wiki.org/crypto/asymmetric/discrete-log/discrete-log/#pollards-algorithm https://baike.baidu.com/item/维吉尼亚密码/4905472?fr=aladdin https://mast.queensu.ca/~kani/lectures/ecc.pdf https://blog.csdn.net/huanghelouzi/article/details/82943615 https://github.com/wy666444/Crypto/blob/master/RSAHitBit/Untitled/sage爆破后八位.sage https://github.com/pablocelayes/rsa-wiener-attack https://en.wikipedia.org/wiki/Wiener's_attack